Every day, we commute from one location to another to engage in different activities. For instance, we employ navigation apps to determine the best and quickest route to our destination when preparing for a journey or service delivery.
Thus, finding the distance between two points is essential in our daily navigation. This provides us with the knowledge of a journey’s length. It also helps calculate fuel consumption, transportation costs, and travel time.
Thankfully, there is a find the distance between two points calculator — a distance tool that helps provide accurate distances during navigation. This guide provides a basic understanding of finding the distance between two points and how to use the calculator.

- Find the Distance Between Two Points Calculator: Understanding the Basics
- Find the Distance Between Two Points Calculator: Using the Pythagorean Theorem
- Find the Distance Between Two Points Calculator: The Straight Line Distance Formula
- Distance Formula Calculator : 3 Common Types
- Find the Distance Between Two Points Calculator: Five Steps To Consider To Get Accurate Results
- Final Thoughts: Get the Best Mapping Experience With Mapize
Find the Distance Between Two Points Calculator: Understanding the Basics
Before we delve into the intricate details of how to use a find the distance between two points calculator, let us understand the basics. The distance between two points is simply the length of a straight line connecting them.
In addition, this straight line is also called a line segment or vector between the two points. This knowledge of distance is helpful when utilizing a find the distance between two points calculator.
Since we have a basic understanding of what distance is, let’s discuss what a point is. A point represents a dot that tells its location in space. It is one-dimensional and has no length, width, or size. Yet it can provide more information. How so?
A point (or dot) has two coordinates — the x-coordinate, and the y-coordinate, represented as (x,y). The x-coordinates are horizontal coordinates, while the y-coordinates are vertical coordinates.
These coordinates have an origin (0,0), and points move away from this origin to attain newer coordinates. For example, suppose a point K has a coordinate of K(3,4). In that case, object K is 3 units away from the x-coordinate’s origin and 4 from the y-coordinate’s origin.
Find the Distance Between Two Points Calculator: Using the Pythagorean Theorem
Now that you understand the words “distance” and “point,” what is an effective way to calculate the distance between two points? Before the invention of a find the distance between two points calculator, mathematicians used the Pythagorean theorem. It is a proven mathematical theorem that continues to provide accurate measurements.
The Pythagorean theorem states, “The square of the hypotenuse of a right-angle triangle is equal to the sum of the square of the opposite sides of the triangle.” Mathematically,
a2 + b2 = c2
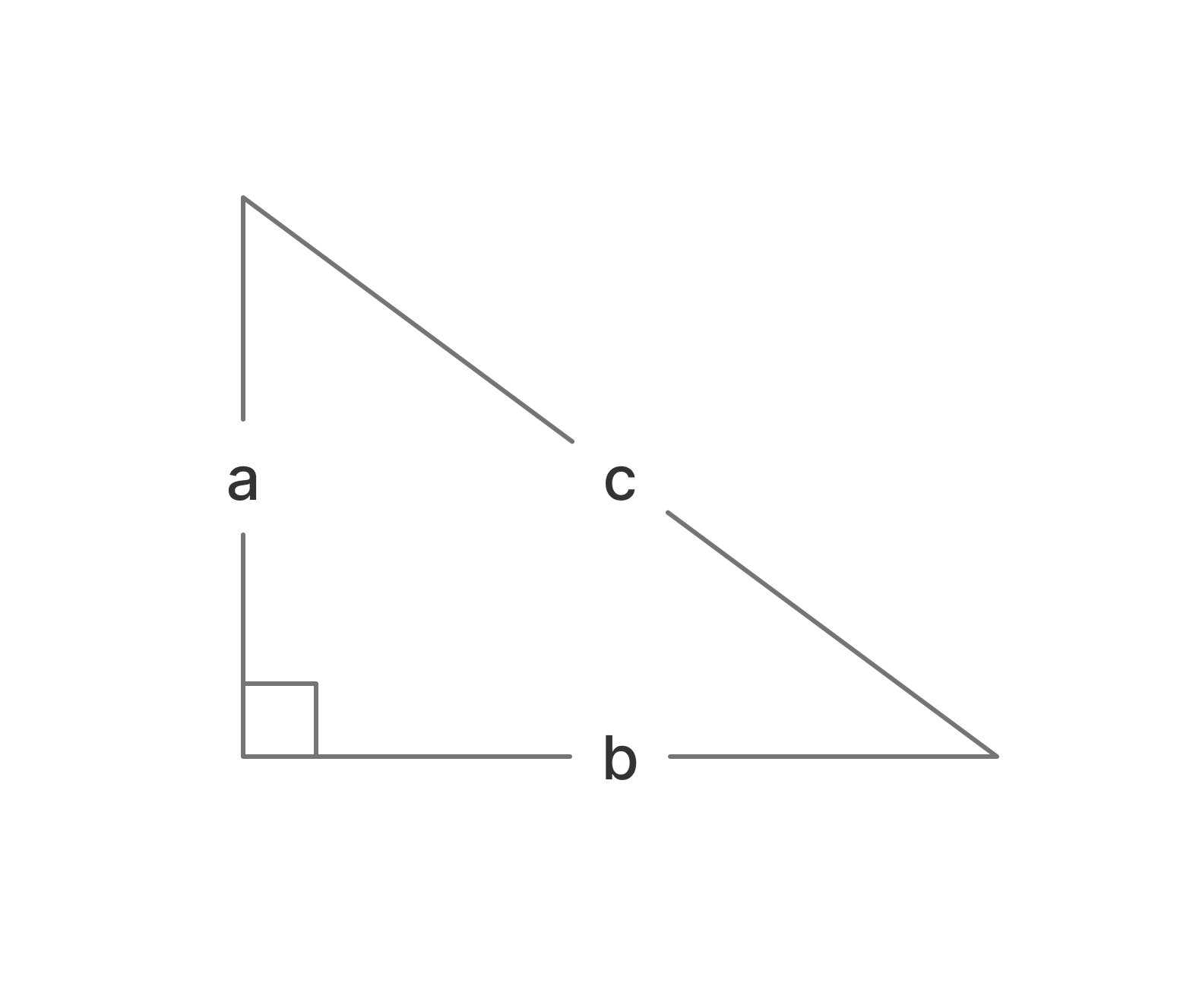
The parameters “a” and “b” are the lengths of the two sides that meet at the right angle, and “c” is the hypotenuse, which is the line segment between the two points.
Remembering the idea of coordinates, point “a” can move some units away from the x-coordinates, and point “b” can move some units away from the y-coordinates. Since they are one-dimensional points, we can calculate the distance between the two points “c” in the equation:
C =√ a2 + b2
Sounds simple, right? For example, let’s calculate the hypotenuse length since the other two sides of the right-angled triangle are 3 and 4 units, respectively.
Since a = 3 units; and b = 4 units
Using the Pythagorean theorem, C =√ a2 + b2
c = √ 32 + 42
c = √ 9 + 16
c = √ 25
c = 5 units.
It is noteworthy that the distance between two points may not always give a perfect number. However, rest assured that you will have the right answers if you apply the Pythagorean theorem correctly. Overall, understanding how the Pythagorean theorem works is helpful when using a find the distance between two points calculator.

Find the Distance Between Two Points Calculator: The Straight Line Distance Formula
The straight line distance formula is important in geometry as a find the distance between two points calculator in a multi-dimensional space. It is similar to the Pythagorean theorem. The distance formula for the straight-line distance is as follows:
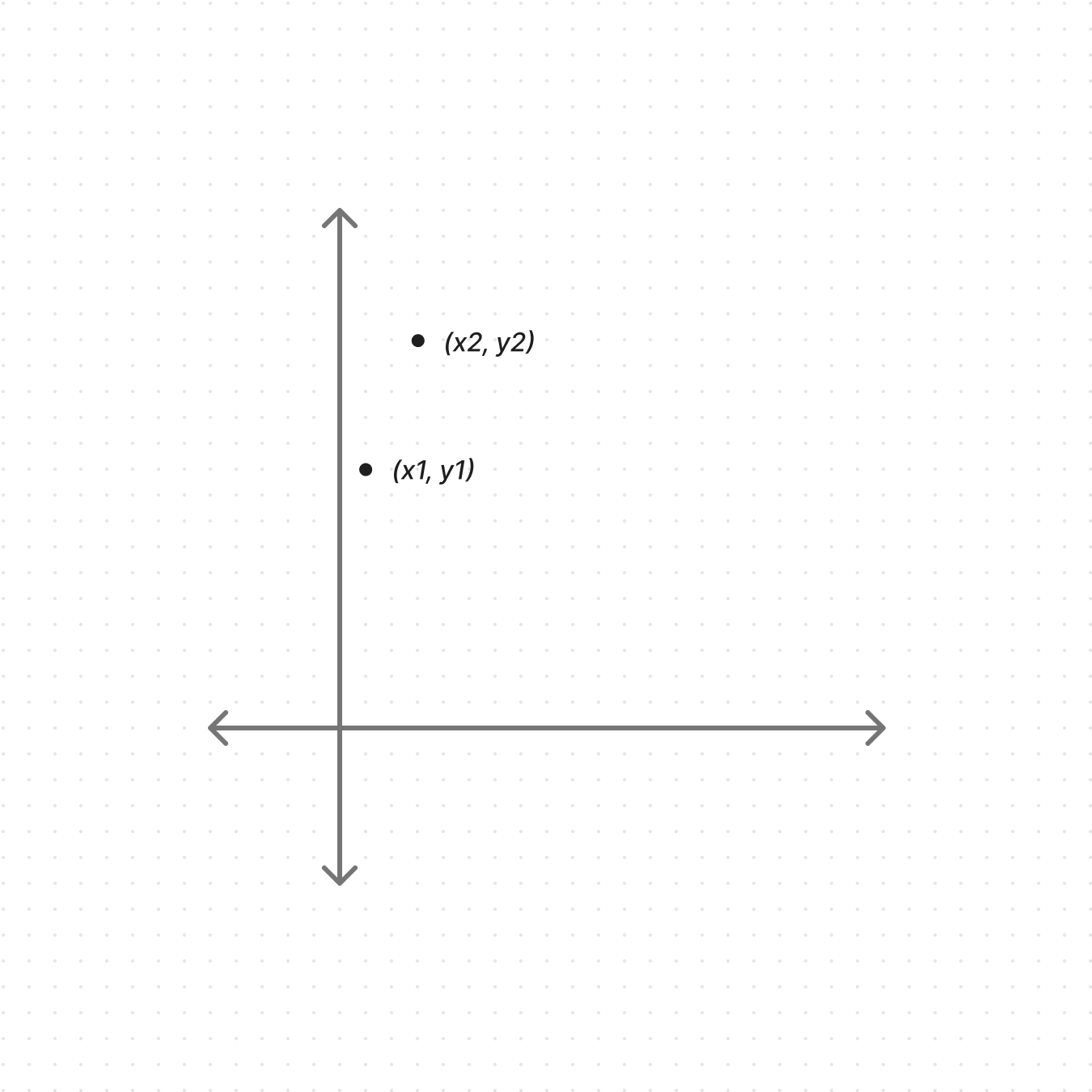
D = √(x2 – x1)2+(y2 – y1)2
In this straight-line distance formula above, the parameter “D” represents the distance between two points (x1, y1) and (x2, y2). These two points represent the horizontal and vertical positions of the endpoints of the line segment.
By subtracting the x-values and y-values of the two points and squaring them, we can find the lengths of the two sides of a right-angled triangle. Then, you calculate the sum of their squares. Then, you can obtain the square root to find the hypotenuse length — the distance between the two points.
To correctly apply this formula, you need to know the coordinates of the two points in the two or three-dimensional space. Once you have them, you can substitute them in the formula and calculate the distance between the two points. Let’s take an example
You want to calculate the distance between points (3,15) and (1,10). Since you have the x- and y- coordinates parameters, you can substitute them into the straight-line formula.
So, given x1 = 1, y1 = 10, x2 = 3, and y2 = 15. We have the straight line distance formula:
D = √(x2– x1)2+(y2– y1)2
Substituting the values and simplifying further,
D = √(3- 1)2+(15- 10)2
D = √(2)2+(5)2
D = √4+25
D = √29
D = 5.385 units
This means the distance between the two points (3,15) and (1,10) is 5.385 units.
Find the Distance Between Two Points Calculator: Applications of the Straight Line Formula
Now you must feel happy knowing how to apply the straight line distance formula without using a “find the distance between two points calculator.” However, is the formula applicable in the real world? Rightly so, as it is practical in engineering, geometry, and navigation.
In engineering, engineers use the formula to calculate the distance between two points in a three-dimensional space. For instance, engineers can calculate the distance between two points on an airplane wing, the length of a cable between two transmission poles, etc.
The geometry formula applies to solve the distance between two points on a line, curve, or other plane surfaces. It is also beneficial in calculating the gradient (slope) of a line between two points. You can solve for a line slope by dividing the change between the y-coordinate (y2– y1) and the x-coordinate (x2– x1) on a find the distance between two points calculator.
Additionally, in navigation, the formula can help calculate the distance between two points on a map. This calculation is essential to determine the shortest and quickest route to take. Further, GPS systems utilize distance calculators to provide geographical positions of a location.
Overall, the straight line formula efficiently determines the distance between two points in two and three-dimensional space. It is impossible to underemphasize this formula’s versatility as it’s a useful tool in many fields.

Distance Formula Calculator : 3 Common Types
Congrats, you can now solve the distance between two points using the straight-line formula. However, it can be mentally tasking when computing and solving complex coordinates. Thankfully, there is an amazing tool — “find the distance between two points calculator.” This distance formula calculator is efficient, reliable, and provides accurate answers.
The find the distance between two points calculator helps calculate larger distances between two points on a plane quickly and accurately. Engineers, navigators, and surveyors can use this tool in their respective fields. But first, let’s discuss the common types of these distance calculators.
- Online Calculators
Thanks to the internet, there are reliable web-based calculators that you can access to help you find the distance between two points. All you need to do is input the coordinate of the two points (x- and y- coordinates) and let the calculator do the arithmetic work for you. - Smartphone Apps
Many distance-calculating apps are available for iOS and Android devices to help you calculate the distance between two points. Many of these apps serve as reliable navigation apps that help determine a location’s geographic coordinates without having to input them manually. - Desktop Software
Suppose you need to calculate varying distances differently. In that case, you may consider downloading a desktop software program. This program has more advanced functions and features than online calculators or smartphone apps. So, it becomes easy to calculate distances in complex dimensions.
Find the Distance Between Two Points Calculator: Five Steps To Consider To Get Accurate Results
Using a find the distance between two points calculator is helpful in many aspects. Yet, there are a few basic steps to consider if you want to obtain accurate results. Let’s take a look at five of them:
- Determine the Coordinates of the Two Points
It would be best to determine the coordinates when using a find the distance between two points calculator. You can get these coordinates via maps, GPS, or online mapping tools. These coordinates display in (x, y) pairs. - Enter the Coordinates into the Distance Calculator
Now that you have the coordinates of the two points, you can enter them into the calculator. Input the coordinates in the appropriate fields. That is, (x1, y1) and (x2, y2) should be in their respective boxes. - Verify the Units of Measurement
It is essential to note the units of measurement available on the distance formula calculator. Many online calculators use kilometers, miles, and feet. Some may employ the S.I. unit of length – meters. Whatever the units, ensure to use the one comfortable to your application. - Verify and Check Your Results
Reverify your coordinates before you begin calculating. After verification, you can run the online calculator to estimate your distance. When the results are out, examine their accuracy. If they seem incorrect, double-check your coordinates and resolve them again. - Apply the Result
After obtaining your desired outcome, you can use this information for any purpose. For instance, if you are going on a road trip, it can help you know the time you’d spend on the road. It can also help you estimate transportation costs and provide the best route.
Final Thoughts: Get the Best Mapping Experience With Mapize
Now you understand that the distance between two points is essential to navigation and geometry. Also, when using a find the distance between two points calculator, you can quickly determine the distance between two points using their coordinates.
If you enjoy mental calculation, the straight-line formula and the Pythagorean theorem are excellent tools for calculating your distance. These formulas can help you obtain the right results.
If you want to create detailed maps, including a find the distance between two points calculator for your business, you should try Mapize. Mapize is a web-based platform that allows you to create custom maps using various data sources and visualization tools.
With little coding experience, you can customize your maps using various markets, layers, styles, and other visually-pleasing features on this mapping platform. Take a look at what Mapize offers and build your first custom map for free.